Défi Mathématique 2005-2006 sur le REP Robespierre

des soluces ...
 décembre 2005
par  Jean-Claude ROLLAND
popularité : 31%

Pour rappel , le sujet du défi 2005-2006 :


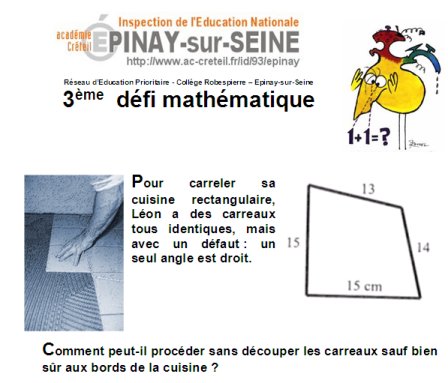
Et les quadrilatères à découper pouvant servir aux manips ...

La solution :

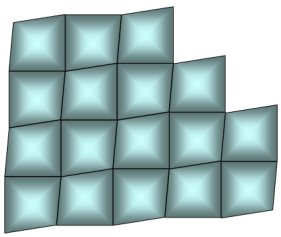
Pour aller plus loin :
– Peut-on paver le plan avec des quadrilatères sans angle droit ?
– Peut-on paver le plan avec des quadrilatères non convexes ?

La solution :

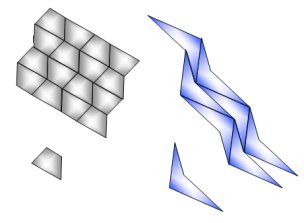
N’importe quel quadrilatère, même sans angle droit, même non convexe, permet de paver le plan.
Maintenant, reste à le prouver mathématiquement !!! Qui s’y essaie ?


Sujet extrait de "100 friandises mathématiques" de R. Ferachoglou et M. Lafond, Irem de Dijon ; éditions Ellipses, 2002


Erreur d’exécution plugins/auto/sarkaspip/v4.2.0/noisettes/document/inc_images_jointes.html

Commentaires  Forum fermé

Logo de Rémi Jacquet
> Défi Mathématique 2005-2006 sur le REP Robespierre
mercredi 4 janvier 2006 à 11h37 - par  Rémi Jacquet

Merci à Henri Mainié, PIUFM pour cette idée de recherche.
Et pour un quadrilatère croisé, qui tient les paris, qui s’y essaye ?

Logo de Sabine M.
> Défi Mathématique 2005-2006 sur le REP Robespierre
vendredi 23 décembre 2005 à 11h17 - par  Sabine M.

N’importe quel quadrilatère, même sans angle droit, même non convexe, permet de paver le plan.
Maintenant, reste à le prouver mathématiquement !!! Qui s’y essaie ?

Cela doit avoir un rapport avec le fait que la somme des angles d’un quadrilatère est égale à 360°. On peut paver le plan si on s’arrange pour placer à chaque noeud chacun des angles du quadrilatère.

samedi 24 décembre 2005 à 15h03

J’avais plutôt pensé à placer à chaque noeud tous les angles de la figure. J’ai réussi en faisant le symétrique du quadrilatère (par symétrie centrale) et en alternant la figure et son symétrique. Là, on n’a pas le problème des différences de longueurs entre les côtés.

Pour les concaves, il y a peut-être une piste en les considérant comme deux triangles, mais je n’ai pas cherché du tout.

vendredi 23 décembre 2005 à 15h35 - par  Jean-Claude ROLLAND

Pas mal ... On pourrait par exemple placer à un noeud les angles droits de la figure du défi.
mais
Deux remarques cependant :
– Cela fait-il nécessairement un motif reproductible permettant de paver le plan ?
– Peut-être est-il possible de placer les figures avec un côté en contact avec un autre plus long ?